【2020百度之星复赛 1005】Battle for Wosneth2 题解

题目大意

  Alice 有 $n$ 血，Bob 有 $m$ 血。Alice 和 Bob 轮流攻击对方，Alice 先手，每次攻击如果命中则对方扣 $1$ 点血，否则无事发生。Alice 命中率为 $p$，Bob 命中率为 $q$。若有人血量 $\le 0$ 则死亡，游戏结束。
  求到最后 Alice 的生命值大于 $0$ 的概率，对 $998244353$ 取模。

  $n,m \leq 10^5$
  多测，$T \leq 10^4$，$\sum(n+m) \leq 5 \times 10^6$
  1s

$$\\$$ $$\\$$ $$\\$$

解法一

  正好前一天做了牛客多校九，H 题生成函数印象深刻，一看这题，好像差不多啊？？

  首先 Alice 恰有 $m$ 次命中。如图，把这 $m$ 次命中看作是 $m$ 块挡板，最后一块挡板的右边不能放东西，而每块挡板的左边都可以插入若干 Alice 失败的攻击和 Bob 的攻击。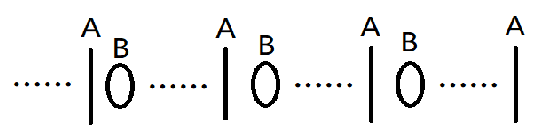

  在前 $m-1$ 次 Alice 命中的右边都先放一个 Bob 的攻击，那么图中的省略号部分，就可以视为若干组“Alice失败攻击+Bob攻击”。

  如果把 Bob 的命中视为 $x$，那么 Bob 的一次攻击可以表示为 $(1-q+qx)$。那么一个省略号就相当于

$$1+(1-p)(1-q+qx)+(1-p)^2(1-q+qx)^2+\cdots\ \ =\frac{1}{1-(1-p)(1-q+qx)}$$

  然后固有的 Alice 的 $m$ 次命中和 Bob 的 $m-1$ 次攻击，多项式为

$$p^m(1-q+qx)^{m-1}$$

  把两个多项式乘起来（注意共有 $m$ 个省略号），得到

$$Ans=\frac{p^m(1-q+qx)^{m-1}}{\left(1-(1-p)(1-q+qx)\right)^m}$$

  那么 $\sum_{i=0}^{n-1}[x^i]Ans$ 就是最终的答案。

  在正常情况下，这里套一个多项式幂、多项式求逆的板子，就 $O(n \log n)$ 过去了。但这题卡 $\log$，必须要线性。
  可以看到，分子分母都是形如 $(a+bx)^m$ 的二项式，那么分子可以二项式展开直接算，分母用泰勒展开：

$$\frac{1}{(a+bx)^m} = \frac{1}{a^m} - \frac{mb}{a^{m+1}}x + \frac{m(m+1)b^2}{a^{m+2}\cdot 2!}x^2 - \frac{m(m+1)(m+2)b^3}{a^{m+3} \cdot 3!}x^3\cdots\cdots$$

  这个也可以 $O(n)$ 算。
  算完之后，要算分子分母卷积的前缀和。这个直接 two pointers 就好了，也都是 $O(n)$ 的。
  于是连多项式板子都不用了，几十行完事。

解法二

  辛辛苦苦推了半天的生成函数，可能只是发现了归一化。。。
  计数姿势太差不配做题

  设初始时人在 $(n,m)$ 这个格子。那么也是捆绑“Alice攻击+Bob攻击”为一组，对一组来说，如果两人都没命中，那么没有意义，直接忽略，因此只有三种转移：$\frac{p(1-q)}{1-(1-p)(1-q)}$ 的概率转移到 $(n,m-1)$、$\frac{(1-p)q}{1-(1-p)(1-q)}$ 的概率转移到 $(n-1,m)$、$\frac{pq}{1-(1-p)(1-q)}$ 的概率转移到 $(n-1,m-1)$。
  显然我们的目标是要走到第一列（即形如 $(x,1)$ 的位置），然后 Alice 最后一击打死 Bob。（当然，在这一格也要考虑两人做无意义攻击的情况，因此概率是 $\frac{p}{p+(1-p)q}$）

  枚举最后一种转移的次数，记为 $x$，那么第一种转移的次数就是 $m-1-x$，第二种转移的次数不超过 $n-1-x$。方案数就可以直接用挡板原理算出来，乘上概率累加起来就是答案。（第一种和第三种次数都确定了，可以直接挡板原理；而第一种的次数+第三种的次数是定值 $m-1$，所以第二种相对于它们来说也是个挡板原理，预处理求个前缀和即可。）

代码

// 解法一

#include<bits/stdc++.h>
#define fo(i,a,b) for(int i=a;i<=b;i++)
#define fd(i,a,b) for(int i=a;i>=b;i--)
using namespace std;

typedef long long LL;

const int maxm=1e5+5;
const LL mo=998244353;

LL Pow(LL x,LL y=mo-2)
{
    LL re=1;
    for(; y; y>>=1, x=x*x%mo) if (y&1) re=re*x%mo;
    return re;
}

int n,m;
LL p,q,A[maxm],B[maxm];

LL fac[maxm],inv[maxm];
void C_pre(int n)
{
    fac[0]=1;
    fo(i,1,n) fac[i]=fac[i-1]*i%mo;
    inv[n]=Pow(fac[n],mo-2);
    fd(i,n-1,0) inv[i]=inv[i+1]*(i+1)%mo;
}
LL C(int n,int m) {return fac[n]*inv[m]%mo*inv[n-m]%mo;}

int T;
LL qq[maxm],qqq[maxm];
int main()
{
    C_pre(1e5);

    scanf("%d",&T);
    while (T--)
    {
        scanf("%d %d %lld %lld",&n,&m,&p,&q);
        p=p*Pow(100,mo-2)%mo, q=q*Pow(100,mo-2)%mo;

        qq[0]=qqq[0]=1;
        fo(i,1,m)
        {
            qq[i]=qq[i-1]*q%mo;
            qqq[i]=qqq[i-1]*(1-q)%mo;
        }

        memset(A,0,sizeof(LL)*n);
        int sz=min(n-1,m-1);
        fo(i,0,sz) A[i]=C(m-1,i)*qq[i]%mo*qqq[m-1-i]%mo;

        LL c=(1-(1-p)*(1-q))%mo, d=(p-1)*q%mo;
        LL invc=Pow(c,mo-2), fm=Pow(invc,m), fz=1;
        fo(i,0,n-1)
        {
            B[i]=fz*fm%mo*inv[i]%mo;
            (fz*=-d*(m+i)%mo)%=mo;
            (fm*=invc)%=mo;
        }

        fo(i,1,n-1) (A[i]+=A[i-1])%=mo;
        LL ans=0;
        fo(i,0,n-1) (ans+=B[i]*A[n-1-i])%=mo;

        (ans*=Pow(p,m))%=mo;

        printf("%lld\n",(ans+mo)%mo);
    }
}