题目大意
有一个长度为 $n$ 的数轴(看作是 $n$ 个格子排成一行),其中有 $m$ 个交界位置被标记了。你要用若干正方形去覆盖这个数轴(如下图),有 3 个规定:
1、正方形边长必须是正整数
2、数轴要被恰好覆盖,即不能有空、不能有地方被多个正方形覆盖。
3、被标记的位置不能是正方形的交界。
一种方案的价值是所有正方形的面积的积。求所有合法方案的价值和。
$n \le 10^9,\ m \le 10^5$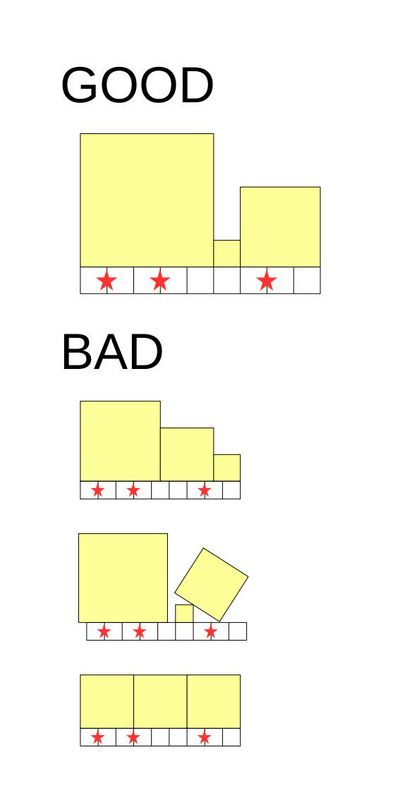
题解
这个很妙啊。。。
首先瞎写一个dp:$f[i]=\sum_{j=0}^{i-1}f[j]*(i-j)^2$,然后发现这个平方非常不好搞。
于是转化模型,把 $x^2$ 看作是长度为 $x$ 的段内,恰好放一个红球和一个蓝球(可以放在同一位置)的方案数。
于是可以设 $f[i][j]\ (j \in [0,2])$ 表示到了第 $i$ 个格子,当前段内有 $j$ 个球,的方案数。转移就是讨论一下 9 个转移,然后写出转移矩阵就可以矩阵乘法了。
至于标记的位置,实际上是那些位置的 $f[i][2]$ 的转移要改一下,不能新开一个正方形。
所以时间是 $O(m \log n)$
代码
1 |
|
