题目大意
这是一道交互题。
有这样一个 $\rho$ 型的有向图: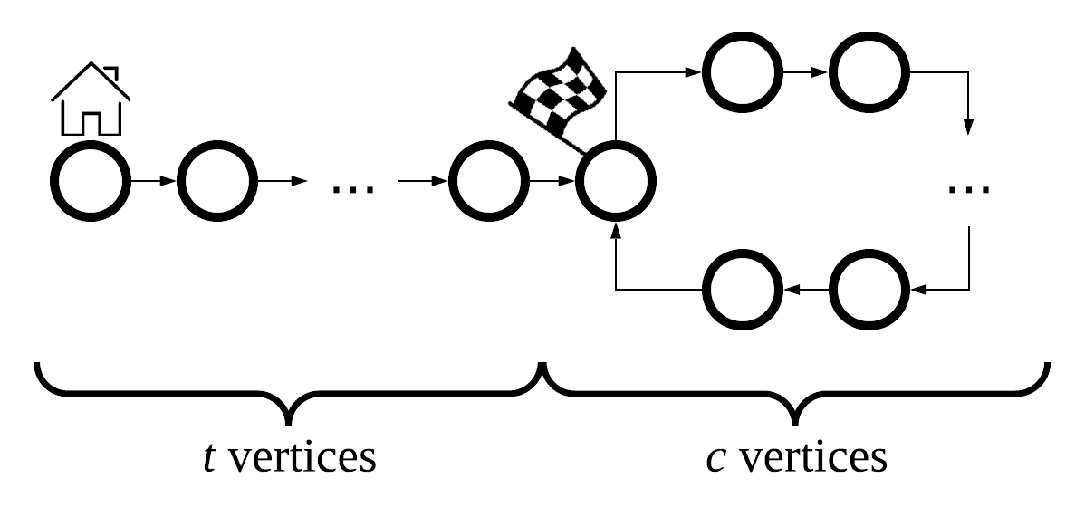
但是 $t$ 和 $c$ 都是未知的。
你有 10 个棋子一开始在起点(标了房子那个),你要把他们都走到终点(标了棋子的那个)。每一步,你可以任意指定一些棋子,让这些棋子都向前走一步。然后电脑会告诉你,哪些棋子是在同一个格子里的。当你认为你把所有棋子都放到终点了的时候,就可以 end 了。
你的步数不能超过 $3(t+c)$。
$t+c \leq 1000$
题解
这肯定是要用 Floyd 判圈了,有意思的是判完圈之后的小分析,这个分析有点妙。
一开始,一个人一次走两步,另一个人一次走一步,那么他们必在环中相遇。
并且慢者在环上最多走一圈。因为如果慢者走了多于一圈,那么快者一定走了两圈了,因此就一定会超过他,不可能跟在他屁股后面转。
设他们相遇的地点离终点距离为 $x$,则慢者的路程为 $t+x$,快者的路程为 $t+kc+x$,$k$ 是快者走过的圈数。
由快者速度是慢者两倍可得 $2(t+x)=t+kc+x$,即 $t+x=kc$,即 $t+x \equiv 0 \pmod{c}$
也就是说,他们相遇后再走 $t$ 步就到终点了。
而剩下的在起点的 8 个人也是走 $t$ 步到终点!!!
所以大家一起走,直到相遇,就行了。
第一个过程的步数,即为快者的步数,不超过 $2(t+c)$,第二个过程的步数恰好为 $t$,所以总步数在 $3(t+c)$ 范围内。
