题目大意
你有无限个这种 S 型的牌(一开始都如左上角那样放置),每次你可以选择一张牌,将其 Rotate,或将其 Flip,或将其放入一个 $N \times N$ 的棋盘。棋盘上不能有牌重叠,被操作过的牌最后都必须放入棋盘。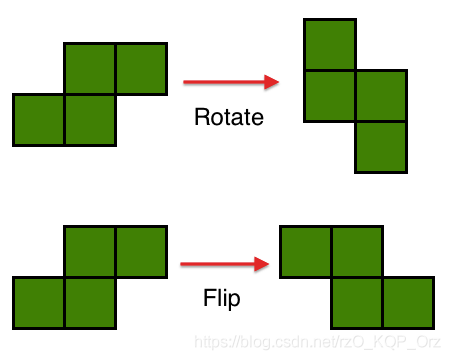
你有一个计数器,每当执行 Rotate 或 Flip 操作的时候,计数器会加 $1$。
现在给你最终的棋盘状态(01 矩阵,表示每个格子有没有被覆盖),求计数器的奇偶性。(保证奇偶性唯一)
$N \leq 50$
这可真是个有趣的问题

题解
为什么奇偶性会唯一呢?到底是什么特征决定了它的唯一性呢?
聪明的 Zayin 想到了斜着看,发现按副对角线的方向来看,贡献为 0 的图形相当于是一个 $(2,2)$ 的覆盖,贡献为 1 的图形相当于是一个 $(1,1,1,1)$ 的覆盖。
于是就有很多办法了。比如先统计出每条对角线的奇偶性,因为 $(2,2)$ 是对奇偶性没有影响的,所以直接拿 $(1,1,1,1)$ 去覆盖这个数组,就知道了有多少 $(1,1,1,1)$。
也可以像题解那样,直接统计下标 $\bmod 4=0$ 的对角线的和的奇偶性就是答案。
