太简单的题,但是又要记录下来做过哪些东西,就写在这里啦~
早搞不搞,等到快退役了才来搞
标 * 的为有价值的题,标 ^ 的为欺诈题,标 - 的为知识点待填坑,标 ? 的表示看别人是这样做的但是没懂为什么
组队训练的题,如果是队友过的板刷题,题面又很长,就会标个“队友说是沙雕题”
AtCoder
AtCoder Grand Contest 028
A:若有解,则 $lcm(n,m)$ 就是最小解
B:对每个 $i$ 考虑删 $a_j$ 时 $a_i$ 造成的贡献,即 $\frac{n!}{|i-j|+1}a_i$
*C:每条边拆成 $a_i$、$b_j$ 两条边,还是找最小圈。那么有三种情况:每个点只贡献 $a_i$、每个点只贡献 $b_i$、其他。对于第三种情况,枚举一个 $i$ 表示它贡献了 $a_i+b_i$,那么剩下的就是选 $a_1,\cdots,a_n,b_1,\cdots,b_n$ 里去掉 $a_i$ 和 $b_i$ 的最小的 $n-2$ 个
*D:设 $f_{i,j}$ 表示最小元素为 $i$、最大元素为 $j$ 的连通块数,通过容斥转移
**E:贪心按位考虑,根据题目性质可以化为一个类似于 LIS 的 dp
看大题解
AtCoder Grand Contest 029
A:略
B:lowbit 相同的分一组,每组从大到小贪心
C:二分,当 $a_i < a_{i-1}$ 的时候就把 $a_i$ 抬升一位,$a_i$ 抬满了就抬 $a_i-1$,注意一些细节
D:两个人的最优策略都是能走就走(先手肯定不能停否则后手一停就结束了;后手尽早走到下一列不会劣于晚些走到下一列)
E:把 $1$ 视为根,那么每个节点需要预处理它的子树“只走权值不超过它爷爷到根的最大权值,能走多少”,记为 $sz_i$,答案就是这个点的儿子的 $sz$ 和加上它到根路径上的其他儿子的 $sz$ 和。这个 $sz$ 的预处理可以简单粗暴数据结构 $O(n \log n)$ 也可以精细地 $O(n)$。
*F:建一个二分图,左边 $1,\cdots,n$ 表示点,右边 $E_1,\cdots,E_{n-1}$ 表示边,左边去掉根以后要存在完美匹配,且从根开始沿”非匹配边-匹配边-非匹配边-……“做 BFS 能遍历所有点
看大题解
AtCoder Grand Contest 030
A:$b+\min(a+b+1,c)$
B:先做出间隔序列(与起点相邻的间隔在序列两端),答案等价于序列上找一个位置叉掉,其中一侧乘上系数 $1,3,5,7,\cdots$,另一侧乘上系数 $2,4,6,8,\cdots$。预处理前缀后缀阶梯,枚举叉掉的位置。
*C:首先找一个偶数的 $n$,奇数行放 $(r+c) \bmod n$,偶数行放 $(r+c) \bmod n+n$,这样会得到 $k=2n$ 的解,如果多了就把最大的 $k+n$ 变回 $k$
D:设 $dp_{i,j}$ 表示一个小的数初始在 $i$、一个大的数初始在 $j$,最终造成的贡献总和,按操作倒序 dp,每次转移是 $O(n)$ 的。最后 $\sum_{i,j | a_i < a_j} dp_{i,j}$ 即是答案
*E:$0 \to 1$ 视为红线,$1 \to 0$ 视为蓝线,那么反转一位相当于线移动一位,答案相当于线的匹配,$O(n)$ 枚举起点的匹配再 $O(n)$ check 即可
看大题解
F:数字从大到小 dp,看成左右括号匹配,设 $dp_{i,j,k}$ 表示考虑了前 $i$ 个数,有 $j$ 个空余左括号,其中 $k$ 个是给定数字作为左括号,的方案数
AtCoder Grand Contest 035
A:必定是 $a_1\ a_2\ a_3\ a_1\ a_2\ a_3 \cdots $ 这样循环,分类讨论共 3 种情况
*B:做一棵 dfs 树,非树边随便定向,树边从下往上定向,判断根是否合法
*C:如图:$n$ 为奇数就大风车,$n$ 为偶数就另外加上 $n$,$n$ 为 $2$ 的幂无解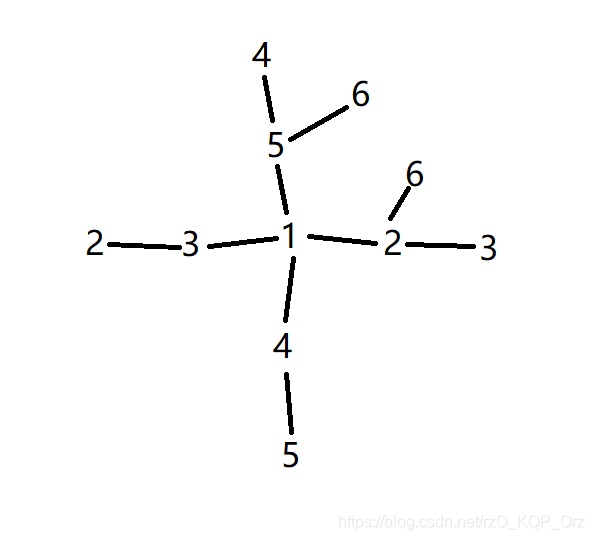
**D:考虑每张牌的贡献次数,设 $f_{l,r,x,y}$ 表示 $[l,r]$ 这个区间,$l$ 贡献 $x$ 次,$r$ 贡献 $y$ 次,的最小代价和。枚举最后吃的那张,发现它的贡献是 $x+y$,就 dp 下去了
看大题解
AtCoder Grand Contest 036
^A:考虑 $(0,0),(10^9,1),(x,y)$,则 $10^9y-x=S$,令 $y=\lceil \frac{S}{10^9} \rceil$
B:考场做法:每个元素向它走到的下一个元素连边,找循环节,暴力跑最后一层
题解做法:连边,然后倍增求每个点走 $2^k$ 层到哪
看大题解
*C:符合条件的序列满足和为 $3M$、单个元素不超过 $2M$、奇数个数不超过 $M$,用组合数和容斥算方案数
*D:设 $p_i$ 为 $0$ 到各点的最短路,dp $p$ 序列的负差分
E:大讨论
AtCoder Grand Contest 034
A:若为 $C<D$ 则先让 $B$ 走到 $D$ 再让 $A$ 走到 $C$,两人分别判断;若为 $D<C$ 则让 $A$ 尽早超越 $B$ 然后分别判断
B:相当于 BC 是障碍物,A 要跳过障碍物到最远的地方去
C:二分,然后推式子发现最多只有一科不是满分,枚举那一科然后剩下的贪心选
AtCoder Grand Contest 037
A:略
B:显然贪心可得最优答案。然后计数,每个第三色有多少种第二色选择,每个第二色有多少种第一色选择,全部乘起来,再乘个 $n!$
*C:倒过来做,如果 $b_i>a_i$ 且 $b_i>b_{i-1}+b_{i+1}$ 那么这个 $b_i$ 必然要被操作,用一个堆找最大的 $b_i$ 来做
*D:问题转化为第一步使得每列包含每行的元素恰好一个。一列一列地确定,每列是一个完美匹配
看大题解
E:第一步找到倒序字典序最小的,然后接下来每次操作可以把结尾的最小字符连续段长度翻倍
*F:按数值从小到大处理连续段(计算连续段的贡献并产生数值 $+1$ 的新连续段),可以把模型改成“如果一个区间合法那么贡献为 $L_i \times R_j$”,在处理连续段时修改 $L,R$ 的值
DISCO Presents Discovery Channel Code Contest 2020 Qual
A:略
B:枚举分界点,答案是左右两边的差的绝对值
C:同一行的草莓先把这行划分掉,然后如果有一行没草莓就复制它上面或下面的分法
*D:解法一:暴力。每个数字是有循环节的(即使用多少个这个数字可以得到它自己),把循环节消掉了就是暴力
解法二:顺序是不影响的,那么考虑把每个数字全部拆成 1,因此进位的影响就是 $\lfloor \frac{数位和-1}{9} \rfloor$
*E:先二分一个位置 $i$ 使得 $[i,i+n-1]$ 和 $[i+1,i+n]$ 的回答是不同的,那么 $i$ 和 $i+n$ 的颜色就确定了,并且 $[i+1,i+n-1]$ 这段区间是两种颜色相同的。剩下的都可以利用 $[i+1,i+n-1]$ 来完成
AtCoder Grand Contest 043
我为什么要交题
A:答案等于从 $(1,1)$ 走到 $(n,m)$ 所经过的最少的连续 $1$ 的段数,$O(n^2)$ dp
*B:先判断答案是奇数还是偶数(看成异或,Lucas 定理算每个数被贡献了多少次),若为奇数则答案为 $1$,否则若原序列有 $1$ 则答案为 $0$,否则把 $2$ 当成 $1$ 再判奇偶
AtCoder Grand Contest 044
NOMURA Programming Competition 2020
AB:略
C:从顶层到底层,逐层确定每层能选多少个点,$O(n)$
*D:图是环套树森林,答案等于 $(n-1)^k-(每种方案下的连通块数)$,而连通块数等于环数,因此要算出每种方案下的环数之和,每个环单独贡献,$O(n^2)$ 求多项式 $\prod(1+size_i)$
F:一个方案合法的充要条件是,对于每一位的第一个 $1$ 和最后一个 $0$,这之间的数在以后的位上都要完全相同。于是 $O(nm)$ dp 一下
E:
ACL Contest 1
*A:思路是每个元素向其左边能到的点连边。但实际上只要做出左边开始的下降序列,那么每个元素只需要在这个序列上连一个区间就行了,可以精细实现为 $O(n\alpha(n))$
AtCoder Regular Contest 107
AB:略
C:行列独立,任意两行如果能换就连一条边,每个连通块大小的阶乘的积就是行的答案,列同理
*D:dp,设 $dp_{x,y}$ 表示当前层有 $x$ 个数、已确定计入答案的有 $y$ 个数,的方案数。同层转移,即 $dp_{x,y}$ 转移到 $dp_{x-1,y+1}$ 和 $dp_{2x,y}$
E:$\forall i,j \ge 4,\ a_{i+1,j+1}=a_{i,j}$,因此只要算前四行和前四列即可
F:
AtCoder Grand Contest 049
A:每个点产生贡献当且仅当它是它及其前驱中最早被选的点,假设它及它前驱共有 $cnt_i$ 个点,可以发现这个概率是 $\frac{1}{cnt_i}$
B:相当于每次可以选择一个 $1$ 前移一位,如果两个 $1$ 撞上了可以一起消掉。因此直接 two pointers 匹配
CDEF:
AtCoder Regular Contest 119
A:枚举 $b$
B:相当于每个字符串的 $0$ 的要按顺序依次匹配
C:观察可得一段序列合法当且仅当奇数位的和等于偶数位的和
*D:建出二分图,每个连通块可用其生成树代替,所有的树要么都保留一个左边点,要么都保留一个右边点
看大题解
*E:只有 $a_{l-1} \le a_l$ 且 $a_r \le a_{r+1}$ 或 $a_{l-1} \ge a_l$ 且 $a_r \ge a_{r+1}$ 的交换才会使答案更优,答案的改变量等于区间 $[a_{l-1},a_l]$ 与 $[a_r,a_{r+1}]$ 的交的两倍,因此问题转化成求最大区间交。
看大题解
F:
AtCoder Regular Contest 141
A:枚举周期长度,取最高位的那一段或其减 $1$ 作为周期。并且考虑 $999\cdots9$(位数比 $N$ 少 $1$)
B:$A_i$ 的二进制最高位必须递增,除最高位以外任选。搬 dreamoon 的 codeforces round 631(div. 1) B 被抓包
*C:考虑“给定括号字符串如何求字典序最小的排列”,那么两个排列分别都可以确定很多的位置,以及留出一些不能确定的连续段,最后这些连续段贪心地做成“()()()…”即可
*D:每个数表示成 $2^c \cdot d$,按 $d$ 归类,则每个类恰好选一个数。求出每个类选的数的上限和下限,则夹在上下限之间的都是可行的
看大题解
EF:
AtCoder Regular Contest 147
A:用堆模拟即可
B:先用类似于括号序的顺序将“奇数位上的偶数”和“偶数位上的奇数”换过来,再将奇数位和偶数位分别排序
C:考场解法:大力猜测存在一个中心点,所有人都尽量往中心点靠。这个中心点的选择只能是线段端点,因此扫描线即可求出答案
题解解法:一顿猛推得到答案为 $\sum_{i=1}^n \max(0,L_i-R_i) \times (n-2i-1)$
^D:$n^m \cdot m^{n-1}$
EF:
AtCoder Grand Contest 059
^A:把子串首尾拼接成环,统计相邻异色的 pair 数,这东西每次最多消除 $2$,所以除以 $2$ 上取整就是答案
B:把数字按出现次数从大到小排序,相同数字之间相当于一个空位可以消除一个答案
CDEF:
AtCoder Regular Contest 156
A:必要条件是 $1$ 的数量是偶数,注意 corner case,比如 $n \le 4$ 且 $1$ 的数量为 $2$
C:以直径中点为根(如果中间没有点就建一个虚点),所有深度的点轮换一位
D:假设每个数的出现次数是 $c_i$,则只考虑 $\frac{k!}{\prod_{i=1}^n c_i!}$ 是奇数的情况,相当于 $c_i$ 只能是 $k$ 二进制下的 $1$ 的组合,dp 一下
BEF:
AtCoder Regular Contest 159
被疯狂 corner case 杀
A:显然 $\bmod n$ 相同的点是可以合并考虑的,特殊考虑 $s \equiv t \pmod n$ 但 $s \neq t$ 的情况
*B:不妨设 $a \le b$,那么每次等价于 $a$ 和 $b-a$ 在操作,但只有 $a$ 会减小。把 $a$ 看成 $a’ \cdot \gcd$,每次操作相当于 $a’$ 减 $1$,所以就看 $a’$ 什么时候减到下一个质因子的倍数
*C:充分条件是 $n|\sum a_i$(因为每两次操作可以使一人相对 $+1$,一人相对 $-1$),且这在 $n$ 为奇数时是必要的,$n$ 为偶数且操作数是偶数时也是必要的,$n$ 为偶数且操作数为奇数相当于一开始随便加上一个 $1,\cdots,n$ 就转化成操作数为偶数的情况了
D:观察可得最优情况下进入一个区间一定是从头开始进入,记 $dp_i$ 表示进入了区间 $i$ 并停在其头部的最长长度,则 $dp_i = \max_{j < i} ( dp_j + \min(r_j + 1, l_i) - l_j)$,树状数组维护一下即可
EF:
Codeforces
Codeforces Round #559 Div.1
A:首先让全部数字都是每行的 $\min$ 值,然后找 $m-1$ 个最大值和 $1$ 个次大值替换成列的 $\max$ 值。
*C:考场解法:想办法做出拓扑图就能得到最终序列了,于是线段树优化连边得到拓扑图,时间 $O(n \log n)$。
题解解法:先判掉 $i<j<next_i<next_j$ 的情况,然后 $i$ 向 $next_i$ 连边,构成一棵树,跑 dfs 序再倒过来。$O(n)$。
**E:先用 $4\log$ 的时间确定每个点的层(类似于整体二分,同一二分层的奇数段一起做,偶数段一起做),再用 $3\log$ 的时间为每个点找父亲(逐二进制位确定每个点父亲,模 $3$ 相同的层一起做)。
Educational Codeforces Round 67
没 AK,丢人~
AB:略
C:要单调不降的区间就全都平着,其他都下降
D:区间排序等价于不断交换相邻两个,因此 $a$ 数组必须包含 $b$ 数组的所有逆序对。随便维护
E:dp,换根
*F:考场解法:设 $f_{i,j,k}$ 表示到了第 $i$ 个元素,结尾为 $j$,共 $k$ 段,的方案数。$k$ 用 AGC019E 的思想优化成 $0\sim 2$,$j$ 扔线段树上,那么转移就是区间乘和加(矩阵)。代码过长,常数过大,请勿模仿
G:费用流直接上。因为最大流只有 50,因此相当于跑 50 次最短路,这是不会 T 的。但还是把你吓得半死甚至丢了一血
Codeforces Round #572 Div.1+Div.2
ABC:略
D1:判是否存在度数为 2 的点,因为度数为 2 的点两边一定是一样的
*D2:选一个叶子为根,从下往上一条边一条边确定
^E:史上最大诈胡题 两边同乘 $(a_i-a_j)$,平方差公式
^*F:设 $f_{i,j,x}$ 表示到了第 $i$ 个数,选了 $j$ 个,最小间隔为 $x$ 的方案数。后两维的有用状态总和为 $O(k \cdot \frac ak)=O(a)$
Codeforces Round #580 Div.1
Codeforces Round #583
A:全买 1$ 和 5€,暴力枚举买了多少个 1$
B:$n+1-\max(0,n-b)-\max(0,n-g)$
C:要么原串合法,要么把最后一个左括号放到开头,要么把第一个右括号放到结尾
D:答案最多为 $2$(封住左上角),因此判断是否存在割点或者左上右下不连通
E:$d_i$ 从大到小做,最长的作为主链,然后贪心填满主链,其他随便挂在主链上
*F:一定能从某个地方割开成链然后从左到右贪心匹配。因此先假设是 $1$ 到 $m$ 的链,每个点的坐标要么是正贡献要么是负贡献,看它前面的 $a$ 和 $b$ 的数量。然后每次把开头的人丢到结尾,可以快速计算对答案的影响。
*G:每行开一个 bitset,若某两行的 bitset 不是包含关系则有解。判断是否存在两行不互相包含只需按 size 从小到大排序然后依次检查相邻两个,用 set 维护
看大题解
H:若直径小于 $k$ 则任意染;若 $k=2$ 则黑白染色;否则直径按 $1$ 到 $k$ 循环染,剩下的枝都有长度限制,在长度限制以内方案是唯一的,超过长度限制则无解
Codeforces Round #584
A:贪心
B:模拟 $10^5$ 次
C:枚举分界的数字,小于它的染 1 色,大于它的染 2 色,这个数字单独判断
D:看成连边,然后答案为 $n$ 减生成森林的边数
E1E2:只有 $\min(n,m)$ 列是有用的,随便状压一下
F:做出最短路图,按拓扑序处理每一个点,这个点相当于选择一条入边然后更新 trie。选择哪条入边更优秀那就看谁是 lca 的小的儿子
G1:设一个数字最左出现在 $l$,最右出现在 $r$,那么 $[l,r]$ 要全部同色。栈+并查集维护一下就好了
**G2:维护这个区间并。给 $[l,r-1]$ 全体加 $1$,那么 $0$ 就是区间并的分界点。用线段树维护这个,然后求区间众数的话再开一棵线段树,每个数的出现次数赋值到最早出现的位置,那么就是个区间最大值
看大题解
Codeforces Round #594 (Div. 1)
A:若第一行存在相邻同色格子,那么后面的行的方案是唯一的;否则等价于第一列的方案数。都是一个递推过去
*B:先把原串循环移位成一个合法括号序(若不存在则答案为 0),然后只有最外层和次外层的匹配括号对才能交换,贡献可以用栈来算
C:大模拟
D:有向图 tarjan 缩环,找到一个没有出度的强连通分量即可作为 jury,其余作为猫
E:一定是第一行从小到大,第二行从大到小,于是最大路径只能是走边界的两条之一。因此问题变成,从小到大排序,前两个数放左上和右下,后 $2n-2$ 个数平分成两个集合,使得最大和最小。$O(n^3\max a)$ dp
Codeforces Round #602 (Div. 1)
*A:任意括号序都是可以被构造的,当前这位不合你意就在后面找一个换
B1B2:询问离线,把元素以大小为第一关键字、位置为第二关键字排序,依次激活,线段树二分查询第 $pos$ 个。
C:二分,用二维前缀和判断
*D1D2:题分为 $h_i=h_{i+1}$(无论如何选都贡献 0)和 $h_i\not=h_{i+1}$(可贡献 1、-1、0)两种,由对称性,正贡献的方案数等于负贡献的方案数,所以非零贡献的方案数除以 2 就是答案
Codeforces Round #614 (Div. 1)
AB:略
C:只有经过 $0$ 的路径是有用的,且必然是在一条路径上放 $0$ ~ $len-1$。类似于区间 dp,设 $f_{u,v}$ 表示 $u$ 到 $v$ 这条路径的答案。
D:集合点一定在某个关键点上,预处理一些东西后任意两个关键点之间的距离可以 $O(1)$ 算。那么就枚举集合点,然后暴力算距离,$O(k^2)$。注意 $k=0$。
Hello 2020
AB:略
C:算每个连续段的贡献
D:按一边的区间排序,set 维护另一边的开始结束时间,判断这边相交的是否有另一边没交,再反过来做一次
E:枚举中心点,剩下的三点只要不在该点的同一侧即可,于是极角排序+two pointers
FG:
Codeforces Round #625 (Div. 1)
A:移项得到 $i-b_i$ 相同的组一队
B:终点出发求最短路图,每个 $p_i$ 依照最短路图的出边进行讨论递推
C:二维偏序随便搞搞
D:一个串的最小表示是:(开头可能有奇数个 1)+(若干个0)+(奇数个1)+(若干个0)+(奇数个1)+…+(结尾一堆1),把这个形状 hash 起来,线段树维护区间 hash
EF:
Codeforces Round #621 (Div. 1+Div. 2)
A:贪心
B:若有步长等于 $x$,则可以一步到位;否则等于 $\lceil \frac {x}{最长步长} \rceil$
C:长度只能为 1 或 2
D:从起点跑一次 bfs,从终点跑一次 bfs,再找 bfs 序相邻的两个关键点连边
*E:枚举分界线(即枚举左集合的最右牛),每种 $f$ 的牛独立算贡献
FG:
Ozon Tech Challenge 2020 (Div.1 + Div.2)
A:两个数组都从小到大排序
B:贪心
^C:考场解法:把所有数按 $\bmod~m$ 分类,先假设都是正贡献算答案,再在原数组求要乘多少个 $-1$
正常解法:$n>m$ 时答案必为 $0$,所以直接暴力
*D:每次询问一个三元组(设 $a-b-c$,则询问 $a,c$),就可以去掉两棵子树
*E:上界就是 $1\cdots n$,第 $i$ 个数最多贡献 $\lfloor \frac{i-1}2\rfloor$。所以先找到最大的 $n’$ 使得 $1\cdots n’$ 的贡献恰好小于等于 $m$,再凑后面的。
*F:答案上限是奇数个数,并且随机选一个数,$O(n)$ 判断 $a_i,a_i+1,a_i-1$ 的质因子,至少 $\frac n2$ 的概率是正确的,随机判断 20 个即可
看大题解
*G:加一个 $a_i=0$ 的点,每条边 $(u,v)$ 赋权值 $a_u+a_v$,答案等价于最大生成树减去点权和。用 Boruvka 求最大生成树,每个点连出去的边用权值的高维前缀和来求
H:
Codeforces Round #626 (Div. 1)
A:前缀和为 $0$ 的位置作为分界点,把序列分成若干段,有问题的段重排
B:按位考虑,每一位相当于要求两个数的和在两个区间内,two pointers
*C:右边的点按照邻集分类,同类求和,不同类求 $\gcd$
*D:dp,设 $f_{i,j,k}$ 表示倒着枚举到了第 $i$ 个数,数字大小为 $j$,有 $k$ 个数字,的最优答案。复杂度分析同那种看起来是 $O(n^3)$ 实际是 $O(n^2)$ 的树形 dp
EF:
Codeforces Round #631 (Div. 1)
A:从左往右放,每个 $l_i$ 放在 $\max(i,\sum_{j=i}^n l_j)$
B:$a_i$ 的二进制最高位必须是递增的,因此最多 30 来个,随便 dp
C:每次贪心找最大的可删除的结点
DE:
Codeforces Round #633 (Div. 1)
A:填平 $\max_{i < j,\ a_i > a_j} a_i-a_j$ 即可
B:最小:若所有叶子的深度的奇偶性相同就是 1,否则是 3;最大:初值为 $n-1$,每当有 $x$ 个叶子父亲相同就减去 $x-1$
C:打表找规律
D:树形 dp,设 $f_{i,0/1}$ 表示以 $i$ 为根的子树,$i$ 选或不选,的最优答案。$f_{i,0}=儿子数量-1+\max\{f_{son,0},f_{son,1}\}$,$f_{i,1}=\max\{f_{son,0}\}+1$,旋根 dp
E:
2020 ECNU Campus Online Invitational Contest
AI:略
C:cdq 模板题
^D:若存在 $0$ 权或所有结点权值均 $\ge 2$ 则直接找一个最小权点即可;否则先找到最长的 $1$ 构成的直径,然后再考虑是否有两条最长的 $1$ 直径用一个 $2$ 连起来,后者用旋根 dp 预处理每个 $1$ 最长能延伸到多少。
F:SA 搞一搞,注意坑点,比如 / 和 . 互换
BEGH:
Educational Codeforces Round 89
BC:略
A:设两种原材料分别有 $a,b$ 个,最终合成了 $x$ 个物品,则有 $a-x+b-x\ge x$,即 $a+b \ge 3x$,因此输出 $\min\{a,b,\lfloor \frac{a+b}{3} \rfloor\}$
D:找到 $a_i$ 最小的质因子 $p$,则 $d_1=p$,$d_2=a_i$ 除以 $p$ 除到不能除为止,若 $d_2=1$ 表示无解
E:相邻两段的分界线是造成方案不唯一的原因,预处理后缀最小值然后随便搞搞
*G:类似于 LCS 一样 dp,预处理第一个串 $len_i$ 表示从 $s_i$ 出发第一次到达空串需要多长。
F:
2020 Ateneo de Manila University DISCS PrO HS Division
ABCDEFG:略
H:设 $M=p_1^{c_1}p_2^{c_2}\cdots p_k^{c_k}$,$N=p_1^{d_1}p_2^{d_2}\cdots p_k^{d_k}$,那么会有 $d_i\prod_{j=1}^k(1+d_j)=2c_i$,枚举 $\gcd(c_1,c_2,\cdots,c_k)$ 的约数作为 $\prod (1+d_j)$ 判断一下合不合法就行了
I:问题转化为问每一个三角形内部包含了多少点。预处理出每条线段下方有多少点即可,注意线段垂直的情况
Codeforces Round #664 (Div. 1)
A:枚举选多少个 $>w$ 的 $a_i$
B:每条边记作 $(i,j)$ 表示它所属的出边集大小为 $i$、它排名为 $j$,而每个点必须恰好选一条入边,因此可以得到所有 $(i,j)$ 之间的互斥关系,然后 $O(k!)$ 枚举
*C:二分,check 的时候求出答案点横坐标、纵坐标、横纵坐标差的合法区间
看大题解
D:简单树形 dp,设 $f_{i,0/1}$ 表示 $i$ 为根的子树,$i$ 往上走是上升还是下降,的最小代价
E:
Codeforces Round #706 (Div. 1)
A:按 $x^2$ 和 $y^2$ 排序
B:出生点必须在顶峰,而且必须在唯一的最长单调段的顶峰,然后讨论一下这个顶峰的较短单调段
*C:$3$ 的倍数的行全染掉,最后一行讨论一下
DEF:
Codeforces Round #707 (Div. 1)
^A:差分序列如果有不相邻的相同值就一定是 yes,因此序列最长为 $O(\sqrt{a})$,取原序列前 $3000$ 个数用 $O(n^2)$ 的方法判断即可
B:二分,枚举每种颜色计算相撞的天数
CDEF:
Codeforces Round #709 (Div. 1)
A:每天优先选第一个人,然后如果发现有人超了,就把选他的天进行调整,调整完行就行,不行就不行
B:提神醒脑小链表
C:单调栈优化dp
*D:先 flyod 求出任意两点最短路,然后反向 floyd 求出任意两点间的最松限制
EF:
Codeforces Round #745 (Div. 1)
A:精细地实现 $O(n^3)$
*B:题目的条件等价于“笛卡尔树深度为 $m$ 的节点恰有 $k$ 个”,大力 $O(n^5)$ dp 冲过去
C:$x+y \le \sqrt m$ 的用一个周期表记录下来,$x+y > \sqrt m$ 的暴力
**E:最短路图上入度为 $1$ 的点是关键点。无修是按最短路排序,每个关键点取前面 $w$ 的最小值或次小值。带修用两个 set 分别维护最小值相同的段和次小值相同的段,以及需要用最小值或次小值的关键点数量。
看大题解
DF:
Codeforces Round #749 (Div. 1 + Div. 2)
濒临紫名了。。。危
^A:傻瓜解法:范围这么小这不直接冲 dp?
聪明解法:要么总和是合数,否则一定能减去一个奇数变成合数
B:一定有点没作为 $b$ 被限制过,以它为中心做个大菊花
C:NO 当且仅当存在一个 X 它的右上也是 X
D:先用 $n-1$ 步求出 $a_n$(依次假设 $a_n=1,2,\cdots,n-1$,用前面的 $n$ 与它遥相呼应),然后用 $n-1$ 步求出其他所有数
*E:YES 当且仅当每个点的询问度数是偶数(想象在询问点对间连边,会构成欧拉图),输出方案只要在生成树上走即可
FGHI:
Codeforces Round #773 (Div. 1)
A:贪心从小到大匹配
B:每次找到第一个与 $a_1$ 相同的 $a_i$,然后在 $a_i$ 后面构建 $a_1,\cdots,a_{i-1}$。提神醒脑大模拟
C:回答 NO 当且仅当它被 0 染色覆盖;回答 YES 当且仅当它没被 0 染色覆盖且有一个 1 染色除了这个位置其他都是 0。用并查集+链表维护 0 染色情况、每个元素左边右边第一个非 0 位置,用线段树看左端点在 $(l_x,x]$ 的 1 染色的右端点最小值是否 $<r_x$ 即可
DEF:
Codeforces Round #831 (Div. 1 + Div. 2)
A:奇数 $+3$,偶数 $+2$
B:令 $a_i \le b_i$,则答案为 $2(\sum a_i + \max b_i)$
C:大胆猜测,一定是排好序后划分成连续的三段,然后 1 3 2 或 2 1 3 这样排。前者 1 肯定是单独一个数,只需枚举 2 3 分界点即可;后者 3 是单独一个数,枚举 1 2 分界点
D:如果一张卡片能放出来,且放出来之后去掉起始点和目标点外仍然有一个空位,那就一定能通过若干步华容道把任意一张卡移到终点
E:简单树形 dp,设 $dp_{i,0/1}$ 表示以 $i$ 为根的子树,$i$ 这个点是否计入贡献,的最大收益
FGHI:
计蒜客
计蒜之道2019初赛第1场
A:略
*BCD:莫比乌斯反演优化 dp
看大题解
计蒜之道2019复赛
A:用线段树求每个数往左的最长下降序列长度及方案数,以及往右的最长上升序列长度及方案数。
B:暴力模拟,当然太暴力是不能过的。
**C:观察得出 $SG(x)$ 等于 $x$ 二进制下末尾 $0$ 的个数。于是先求出 $cnt[i]$ 表示 $SG$ 值为 $i$ 的 $x$ 有多少个,然后像快速幂一样自己 FWT 自己,共 $\log$ 次 FWT。
D:贪心。由于每次要求最大值的区间是往右滑窗的,所以可以用单调队列。
E:贪心。
JZOJ
2019.08.04【NOIP提高组】模拟 A 组
t1:递推
*t2:化成 $x^m \equiv x~(\mod n)$,每个质因子下暴力解,再把解数乘起来
*t3:解法一:LCT
解法二:用两个倍增数组,一个存链上最小值(忽略方向,启发式合并),一个存方向
2017.11.09【NOIP提高组】冲刺A组
*t1:NOI2015寿司晚宴(每个数最多含有 8 个小质因子和 1 个大质因子(以 $\sqrt n$ 分大小),按大质因子分类,状压小质因子 dp)
t2:边双缩起来得到一棵树,把直径连起来
t3:保留初始 mst 的 $O(n)$ 条边,以后每次 add 直接重建 mst
HNOI2018
*D1t3(5657):11 条非树边 22 个关键点,建虚树,虚树上儿子对父亲的贡献系数可以预处理,然后 $O(2^{11})$ 枚举每条非树边的下点选不选,在虚树上做 dp
d2t1(5658):预处理每个点只往左和只往右最远能到达哪里,然后从左往右每个点暴力扩展(要一段一段地跳),是线性的
*D2t2(5659):转化成树的问题,每个点是一个权值序列,每次找平均权值最小的序列,并到父亲的末尾去,用堆+dsu 实现
NOI2020全国统一省选
*D2t3(6741):矩阵树定理,把每条边视为 $1+wx$,那么 $\det$ 就是生成树的边权和。$\gcd$ 利用 $\varphi * 1=id$ 拆掉
散装
4703:物品做背包,钱袋子 meet in the middle,注意折成 $20+10$ 复杂度最优
4829:蚂蚁问题,每次询问二分
*4847:若 $x$ 到 $y$ 的路上经过奇环,则一定可以,否则看路径长度的奇偶性。用广义圆方树
*4939:左端点从左往右移,线段树维护右端点。每次左端点右移就相当于结算一些段
看大题解
5001:状压 dp,设 $f_s$ 表示 $s$ 这个集合的字符串的 trie 大小,肯定先把这个集合的公共字母全部提取出来,然后枚举一个分割来转移
100003:树边从深度小的连向深度大的,返祖边从深度大的连向深度小的,最大费用循环流
BZOJ
^3083:换根是吓人的,实际上根据 $id$ 和 $root$ 的关系可以把询问拆成至多两个 dfs 序区间,用链剖+线段树维护区间最小值
*5016:每个询问 $(l_1,r_1,l_2,r_2)$ 可以拆成 4 个前缀询问 $(r_1,r_2)-(l_1-1,r_2)-(l_2-1,r_1)+(l_1-1,l_2-1)$,然后莫队
Ynoi
4810:莫队,加法和减法用 bitset 解决,乘法暴力枚举 $x$ 的因数判断
*4811:链剖,线段树维护每个区间从左到右、从右到左、全 0 进入、全 1 进入得到的结果,询问按位贪心
*4939:莫队求每个区间的 bitset,需要一些技巧
看大题解
4940:bzoj3083+bzoj5016
UOJ
Goodbye Jihai
t1:按价格排序,那肯定是买便宜的然后白嫖贵的,所以前面做背包,枚举最后一个买的之后后面的按质量贪心选
**t3:最优一定是从一个点出发左右扩展,且一个点往一边扩最多有 $\log$ 段,因此有用的区间最多 $O(n \log n)$ 个,在这些上面做区间 dp
看大题解
UOJ Easy Round #9
A:正常情况下以起点为中心极角排序转一圈就好了,但是有可能所有点在起点的同一半平面上,但这可以从一侧开始走,走到 $n$ 时递归成子问题
*B:每个颜色块做 bfs 到达其他所有点的最短距离,用 bitset 求出对于其他每个点,有多少该颜色的点能沿最短路图到达它,能的点到它的距离就是最短距离,否则是最短距离 $+1$
C:
Goodbye Xinchou
*A:解法一:特殊讨论答案为 1 或 2 的,然后 dfs 求答案为 3 的,剩下的就是答案为 4 的。
解法二:特殊讨论答案为 1 或 2 或 3 的,剩下的就是答案为 4 的。但是在赛场上 FST 率极高。
B:给胜者向负者连边,这样形成了一棵树状数组那样的树,且奇数层填正号,偶数层填负号。那么贪心填就好了,找找规律,最后是 $O(n)$ 实现。
CDE:
UOJ Round #30
A:把图按拓扑序画下来,每层最多两个点,相邻层要全连,使劲递推即可
BC:
LOJ
*2509:转化成树的问题,每个点是一个权值序列,每次找平均权值最小的序列,并到父亲的末尾去,用堆+dsu 实现
*2978:“每个数包含奇数个哪些质数”可以看成 01 向量,做成线性基。区间太长时每个小质数都是基
看大题解
*2980:每个位置是一个向量 $[A_i,B_i,C_i,1]$,操作都是矩阵乘法,用线段树维护。
看大题解
CometOJ
2019 Wannafly Winter Camp Day5
Comet OJ Contest #6
A:略
B:$O(n^3)$ 暴力 dp。
C:考场解法:扫描右端点,用线段树维护左端点的答案。其实就是要维护左端点到当前右端点之间,一共有多少个度数不为 $0$ 的点。时间 $O(n \log n)$。
$O(n)$ 做法:求所有区间的连通块数和,转化成计算每个点的贡献。让一个连通块在它的 LCA 处被统计,那么就是说:一个点,它的父亲边被砍掉了,它的儿子边至少有一条。
Comet OJ Contest #8
AB:略
C:不管什么顺序都是 $\sum_{i=1}^{n-1} b_ia_{i+1}$,再枚举一个区间乘 $k$
D:枚举右端点,线段树维护左端点答案
E:枚举 $f$ 的值为 $i$,那就是求 $\lfloor \frac{n}{i^2} \rfloor$ 以内有多少个数没有平方因子,容斥反演一套打下去
Comet OJ Contest #13
AB:略
C:维护一个 $1$ 的并查集,每行再用一个并查集维护每个元素最右边的 $0$ 在哪里
D:递推(设 $f_{i,0/1}$ 表示到了第 $i$ 个元素,$\sqrt a$ 选了奇数个还是偶数个,的贡献),矩阵乘法加速
E:枚举一条边经过的一个点,然后得到其余每个点在什么斜率下会被覆盖
*F:大力分块
HDU
2021CCPC华为云挑战赛
A:按 $a_i$ 从大到小贪心放
B:数据随机,枚举 2000 个 $k$,只判断序列前 20 个元素即可
C:多重背包
DEFG:
牛客
东华大学2020年程序设计竞赛
ABC:略
D:PreFinals 2020 Day3 F 从小到大一段一段地合并,行就行,不行就不行
F:最后结论是,若存在一个串里面 1 的个数是奇数,则先手必胜,否则先手必败
G:dp,设 $f_i$ 表示考虑了前 $i$ 个数的最优答案。转移只需考虑最后一个 $0$ 和最后一个 $-1$
H:建主席树,表示每个点到根路径上的值域线段树,每次询问二分。强行卡常不可取
K:暴力(先 bfs 求出所有的 country,然后每个 country 边界点暴力往四周遍历,碰到别的 country 点就 break)复杂度是对的(隐约感觉,交了能过,还不会证
EIJ:
2020牛客多校(第一场)
一吨 paper 题加一两个用脚造数据的题
F:队友说是沙雕题
A:考场解法:(队友搞的)令 $a_i=s_i \oplus s_{i+1}$,对 $a$ 数组求 SA,然后再怎么排个序
题解解法:令 $c_i=\min\{j-i\ |\ j>i,\ s_i=s_j\}$,对 $c$ 数组求 SA 就是答案
*B:CF Round 614 Div1 D 评论区粉兔 先求出第一步往哪棵子树走,走过去之后,这棵子树就只有素数间隔那么多个元素了,建虚树找重心
D:KKT 条件
H:先假设容量为 $1$,不断 SPFA 单路增广求出从源点到汇点的第 $i$ 个流量所需的费用。每次询问等比例放大,相当于每 $u_i$ 个流量为一种费用,问前 $v_i$ 个流量总共需要多少费用,$O(1)$ 回答
*I:带花树,每个点拆成 $d_i$ 个点,每条边也多拆两个点出来,答案等于 $最大匹配-边数$
J:β 函数
CEG:
2020牛客多校(第二场)
D:略
^C:解法一:找到重心,然后叶子按 dfs 序排序,头尾匹配
解法二:任找一个非叶节点作根,然后叶子按 dfs 序排序,假设有 $s$ 个叶子,那么 $l_i$ 跟 $l_{i+\frac s2}$ 匹配
*E:答案可以表示成 $选18个数以内得到的答案+若干个“选18个数以内组成0”$,先做 18 次 FWT 算出任选 19 个数以内的所有情况,然后后面的 dp 上去
F:单调队列求滑窗最大值。注意线性预处理 $\gcd$,这里至少有两种方法
G:大力 bitset 冲过去
*H:两种情况,若 $x$ 是最大值,那么找 $x$ 的两个前驱;若 $x$ 不是最大值,则找一个 $a[i]>x$ 使得 $a[i]-a[i-1]$ 最小。用平衡树维护
I:看作在网格图上从 $(1,n)$ 不能走到主对角线,那么就是 bzoj 狼抓兔子,最小割用最短路实现
J:对于输入的每个环长 $r$,把这个环“拉大” $k \bmod r$ 倍即可,$k$ 是质数会保证操作一定可行
K:枚举第二个圆上的点,推出积分式子,然后辛普森
AB:
2020牛客多校(第三场)
AL:略
B:队友说是沙雕题
C:先找到长度为 $9$ 的边,然后看比它的前驱后继哪个长,结合叉积判方向
D:分两种情况讨论,若 $n$ 大 $m$ 小,则左边下边铺一个 $L$ 型,剩下的点从左下角往右上角拓展;若 $m$ 大 $n$ 小,则做一条直线+若干散点
*E:把两个匹配的边都连上,会发现构成若干个大小为偶数且大于等于 $4$ 的环,于是就可以 dp
F:若 $a,b$ 能约分则随便构造;否则若 $b=1$ 或 $b$ 只有一种质因子则无解;否则 exgcd
*H:按位考虑,假设当前要排序的区间是 $[l,r]$,取一个最高位的修改操作使得它会把这个区间劈成两半,然后递归下去
GIJK:
2020牛客多校(第四场)
*A:从小到大枚举最大距离 $x$,算出这个距离最少需要多少关键点(每次找深度最深的点,它的 $x$ 级祖先为根的子树删掉,用线段树实现,关键点数量是 $O(\frac nx)$ 的),然后 two pointers 求答案
B:队友说是沙雕题
*C:倒着插入字符,维护前缀最大值,会发现形成了一个 trie(大小不超过 $10n$),于是 trie 上建 sam
*D:三种情况:1、一位一位来,发现答案 $\le 9$;2、首段不超过 $30$,dp;3、首段超过 $30$,发现划分方案是唯一的
*E:从小到大枚举当前的 $x$,比 $x$ 小的记作 $0$,比 $x$ 大的记作 $1$,那么就是问 $x$ 的左右两边是否能消成特定数字;暴力的话可以从左往右用栈贪心,那么快一点就用线段树维护一下某段对栈的影响
F:可以判断 C、D 分别在 AB 中垂线的左边还是右边,然后讨论
H:倒序考虑所有质因子的倍数,没匹配过的按其最小质因子从大到小贪心匹配
**J:类似 Kruskal,并查集维护每个连通块的大小、相邻连通块的大小之和,其中相邻连通块的大小之和用启发式合并邻居表+根号平衡
看大题解
G:
2020牛客多校(第五场)
F:略
D:队友说是沙雕题
A:一定有一个传送门是随身带着的,因此 $O(n^3)$ dp
B:任选一个点作根,每个点求出它到根的异或和 $s_i$,会发现任意两个点之间连边的话权值一定是 $s_i \oplus s_j$,那么就是个最小异或生成树
*C:二维生成函数推一推
E:等价于 $[1,2,\cdots,n]$ 经过这个置换会得到多少不同的排列,因此是所有环长的 $lcm$,要高精度
*H:每个右端点有 $O(\log a)$ 个有效左端点,总共 $O(n \log a)$ 个有效区间(看作平面上的点,点权为 $1$),如果两个区间 $[l_1,r_1]$ 和 $[l_2,r_2]$ 满足 $l1 \le l_2 \le r_1 \le r_2$,那么新增一个区间 $[l_1,r_2]$,点权 $-1$,每个询问树套树二维数点
I:$ans=\frac 23$,方法为按对角线划分,连着两条对角线放 H,然后一条对角线交替放 E 和 G,边界点如果不合法就不放了,不影响极限
K:队友说是大模拟
GJ:
2020牛客多校(第六场)
排列题大作战。。。
*A:大胆猜想可以证明每次选一个环来操作是最优的,因此设 $f(n)$ 表示环大小为 $n$ 的操作期望,推一下式子发现很简单
*B:解法一:看样例找规律,大胆猜想大胆写,要么怂B要么一血
解法二:每个向量加进来的时候都不属于之前的空间,因此概率为 $\prod_{i=0}^{n-1} \frac{2^n-2^i}{2^n}$,化简一下可以递推
C:队友说是沙雕题
E:若 $n$ 为奇数,则 $k=0,ans=[1,n-1,2,n-2,\cdots,n]$;否则 $k=\frac n2,ans=[n,\frac n2,1,n-1,2,n-2,\cdots]$
G:从左上到右下的副对角线、每条副对角线从右上到左下进行染色,且显然下标为偶数的副对角线,再染下标为奇数的副对角线
H:数位 dp,设 $f_{i,sx-sy,0/1,0/1}$ 表示从高到低到了第 $i$ 位、$a$ 数位和减去 $b$ 数位和为 $sx-sy$、$a$ 是否小于 $b$、$b$ 是否小于 $n$,的方案数
J:预处理出每一轮剩下的数字里要选第几个,然后线段树求出置换
K:随便 dp 一下
DFI:
2020牛客多校(第七场)
^A:搞一个会 T 的 dp,比如设 $f_{i,x,y,sx,sy}$ 表示现在到了 $(x,y)$ 的位置,放了 $i$ 个点,之前的点横坐标和为 $sx$,纵坐标和为 $sy$,的最优答案。然后打表
B:队友说是沙雕题
*C:第一个操作看成全体 $+w$ 然后把 $x$ 丢进一个 multiset 里;第三个操作看成询问某个点到 multiset 里所有点的距离和,链剖解决;第二个操作看成单点询问和单点加法
D:打表发现只有 $1$ 和 $24$ 是合法的
**E:设 $dp_{i,(j,pj)}$ 表示目标树的第 $i$ 个结点,匹配模板里的结点 $j$,$i$ 连向父亲的边匹配 $j$ 连向 $pj$ 的边,的最小代价。转移是个 KM,用最短路快速退流
看大题解
*G:先 dp 出一个普通矩形的拓扑序数量,然后第一个矩形倒着 dp,设 $f_{i,j}$ 表示第一个矩形上排从右到左到了 $i$、下排从右到左到了 $j$ 的方案数,普通的转移是个挡板,$f_{i,i-1} \to f_{i-1,i-1} \to f_{i-1,i-2}$ 特殊地 $O(n)$ 转移一下(这样的情况只有 $n$ 次,不会 T)
H:必有 $n=xk$ 或 $n=xk+1$,而 $x$ 和 $k$ 必有其一是 $\le 10^6$ 的,枚举这一个算另外一个
*I:答案为一个点的贡献 $\times n$,枚举一个点的度数,用 prufer 序 dp 出方案数
J:想办法连个图出来,跑足够多次传递闭包
F:
2020牛客多校(第八场)
*A:等价于求连通块个数,大力 LCT
*D:$n \bmod p$ 的部分分布在 $a_1,\cdots,a_{p-1}$,方案为整数拆分;其余部分考虑分在 $a_1$ 和 $a_p$。
看大题解
E:枚举 $m\cdot a_1$(枚举总量是 $O(n \ln n)$),这会对 $[ma_1+3,ma_1+2m-3]$ 这一段的 $n$ 产生一个类似于等差数列的贡献,那么打上差分标记,再求个前缀和,就得到答案了
G:大力打牌题
I:视为 $a_i$ 与 $b_i$ 连边,每个连通块如果有环那么每个点都能选上,否则恰有一个点不能选
K:第一问就是 $b_1$,第二问贪心选最大的前缀和
BCFHJ:
2020牛客多校(第九场)
A:队友说是沙雕题
B:树形 dp,收益$\ge$代价的按代价从小到大做,收益$<$代价的按收益从大到小做
*C:求“长度平方”即考虑点对的贡献,右点往右移,用线段树维护左点的贡献,这是个区间 $\times 2$ 和区间求和
^E:推推式子,for 一遍的事 把你骗去写类欧了
F:简单的滑窗处理
*G:考场想法:大力树链剖分,没写完不知道行不行
题解解法:时间分治+可撤销并查集+维护一个连通块的相邻连通块大小之和,相当于连通块在树上的“儿子”之和 + “父亲”
*H:每个间隔都是形如 $\frac{1}{1-cx}$ 的多项式。分治算出分母,然后多项式求逆
I:找最小的非 $0$ 数作为其中一个乘数,剩下的作为另一个乘数
J:$O(n^3)$ 随便搞搞
K:枚举终点
GL:
2020牛客多校(第十场)
*A:$\times 2$ 关系会形成很多个环,一个环 $\times 3$ 会通向另一个环,因此可以直接贪心 $\times 2$,不行就 $\times 3$
D:
E:倒着维护一个单调递增的栈
J:day7E 弱化 树形 dp 用 KM 转移
BCFGHI:
2021牛客多校(第十场)
A:给字符串排序建 trie,trie 上要合并掉单链
*D:通过直径中心往外加叶子的顺序进行 dp
*E:六合一很好玩吗 king、Rook 是平凡的,Knight 只需记录离边界的距离,Queen、Bishop 维护 $cnt_{i,j}$ 表示有 $j$ 侧是 $\ge i$ 的维数。
F:队友说是沙雕题
G:如果选定一群人最后或者的话,概率是可以列个式子的,然后再推个容斥系数
H:按 1 的奇偶性染色
*J:每个点能照亮的是一段区间,所以是环形线段覆盖,破环为链然后倍增
*K:枚举竖直方向步数把两维独立,然后每一维用暴力+对称容斥进行根号平衡
BCI:
2021牛客多校(第四场)
*A:每个子树的生成函数是儿子的积加上 $\frac{1}{1-x^{a_i}}$ 再减去前 $c_i$ 项
*B:设 $a_i$ 表示序列长度大于 $i$ 的概率,则 $a_i$ 的生成函数为 $\prod_{i=1}^n \frac{1}{1-p_ix}$
C:假设 $a$ 最小,先让三个串开头都是 ‘a’,问题归约成 $<0,b-a,c-a,n-a>$,让 $s_1$ 剩下的全放 ‘b’、$s_2$ 剩下的全放 ‘c’、$s_3$ 根据限制放 ‘b’’c’’d’ 即可
*D:地方撒
E:以 1 为根,产生 $n$ 个限制,每个限制形如 $x \oplus w_i \in [l_i,r_i]$,这对 $x$ 来说有 $\log$ 个合法区间,所有这些区间覆盖在数轴上,被覆盖 $n$ 次的位置就是合法的 $x$ 取值
^F:无论如何操作对于“点数+边数”都是减少奇数个,因此判断 $n+m$ 奇偶性即可
*G:考虑组合意义,转化成给 $D+nk$ 个有标号球染色,每种颜色至少 $k$ 个,的方案数,容斥 dp
*H:枚举 $\gcd(j,k)$ 推式子
IJ:队友说是沙雕题
2021牛客多校(第二场)
CDFIK:队友说是沙雕题
*B:列出式子来,组合数求前缀和用递推
*G:如果区间 $A$ 包含了区间 $B$,那么区间 $A$ 要么自成一组,要么与 $B$ 同一组(相当于扔掉),因此没有包含关系的区间就是滑窗的,排序,dp
J:每个质数的贡献单独考虑,是 $p^{\sum_{c}\binom{p^c的倍数的数量}{c}}$,过程类似埃式筛,要用欧拉降幂
L:按度数是否 $>\sqrt{2m}$ 分为大点和小点,小点更新时将更新信息推送给邻居,每个点询问的时候从小邻居获得更新信息(什么时候超过了自己),从大邻居的预处理中获得什么时候超过了自己
AEH:
Astar
Astar 2019 复赛
1001:显然每个节点要么选 $l_i$,要么选 $r_i$
1002:假设 $c \leq a \leq b \leq d$,那么 $\frac{a-c}{b-a}$、$\frac{d-b}{b-a}$ 必须是整数,且两者二进制下的 $1$ 恰好错开
1003:中序遍历,若根最小且左右 $size$ 不同,则谁 $size$ 小谁先走,否则谁含有标号最小的点谁就先走
*1004:设 $f_{i,q}$ 表示第 $i$ 个数,值选在 $q([l,r])$ 这个区间时,每一种选法的方案数。区间数量总共是 $O(n)$ 的
Astar 2020 初赛(第一场)
1001 1002 1003 1004:略
1005:每个黑格子都可以独立算贡献,最终推式子得到答案为 $\frac{a_1+a_n}{4}$
1006:二分第 $k$ 小的权值,然后算小于等于这个权值的点的权值和,再减去多的
*1007:二分时间 $t$,于是所有格子按照“能到达哪些窗户”分为 $2^k$ 类,算出每一类的数量,网络流判一下
*1008:powerful number
看大题解
Astar 2020 复赛
1001:$m-(\frac{100m}{p}-1)\frac{q}{100}$
1002:+1 只能用一次,枚举用来 +1 的前缀
1003:最大值:每 $l$ 个数,最后的 $k$ 位倒序放最大的。最小值同理
*1005:解法一:Alice 的 $m$ 次攻击视作 $m$ 个挡板,那么每个间隙都是一个生成函数。最后要泰勒展开,不能上多项式板子
解法二:dp 推一推,是个简单的组合数计数
看大题解
1004 1006:
Code+
Code+第七届
其他
学军信友队趣味网络邀请赛
A:
B:方法一:点分
方法二:直接每个点找一个离它最远的点(在直径上)算答案即可
*C:区间 dp,先用完全背包算出 $d_x$ 表示走 $x$ 距离的最小花费,然后 dp 时一个区间的转移必然要转移到这个区间被划分开,因此有用的区间一定是一个段的前缀或后缀,因此有用的区间是 $O(n)$ 的
D:$h_m=$最大的 $2^k$ 使得 $2^k|m$。枚举 $2^k$ 算贡献,转化成求 $[1,n]$ 每个数的约数个数和,分块+卡常
第三届上海理工大学程序设计竞赛
ABC:队友说是沙雕题
^D:一条边 $(x,y)$ 的权值等价于 $\text{make_pair}(\max(x,y),\min(x,y))$,因此 MST 也是唯一的
E:Dijkstra 求出排列 $[1,2,\cdots,8]$ 到其他排列的最短路,然后对于原序列,枚举一种置换,算答案
*F:构造 $k=1$ 的时候 $(2,2\times3,5,3\times 5)$,$k>1$ 的时候把这个东西复制 $k$ 份,然后修正,即每组的 $2\times3$ 不能抢后面的 $5$、每组的 $3\times5$ 不能抢后面的 $2$。
G:单调栈
H:每个格子的贡献取决于最后一次修剪
*I:prufer 序 dp,初始连通块缩起来当一个点考虑
看大题解
*J:询问所有的 $2\times2$、$2\times3$、$3\times2$ 即可知道任意一对相邻格子是否相等
*K:$k=2$ 时,维护奇数位一棵 treap 和偶数位一棵 treap,操作一个区间相当于两棵 treap 互换子树;$k=3$ 时同理,维护 6 棵 treap 即可
L:只需最后两位是 4 的倍数即可。注意 corner case
M:插头 dp,一个格子有 4 种状态(石头、水、没水的甘蔗、有水的甘蔗)
福州大学第十七届程序设计竞赛
ABCDEF:略
I:先挖掉一种颜色,剩余两种颜色合并连续段,则只有 $O(n)$ 种情况,然后组合数算一下方案数
*J:可删除线性基求交
看大题解
GH:
